 |
| Igor Balla for Quanta Magazine |
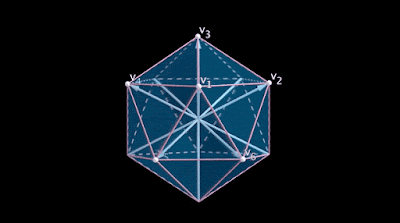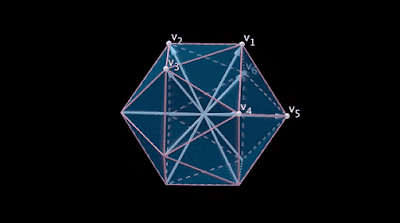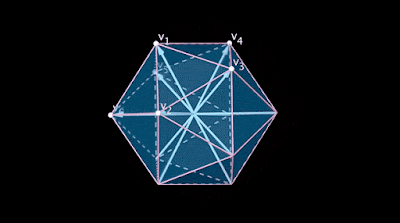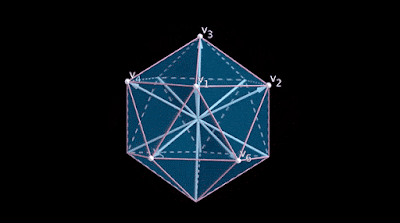
Imagine a set of many lines as in a dream. The lines intersect at a point and radiate outward. There’s something perfect about the way they’re spaced that you can’t quite put your finger on. You start counting them, but before you can finish you wake up with a question hanging on the fringe of your mind: Just how many were there?
For at least 70 years, mathematicians have been trying to answer a question like that one. The sets of lines they’re interested in share a basic feature: Any two lines from the set intersect to form the same angle. Such sets of lines are called “equiangular.” Mathematicians want to know just how big those sets can get as you move past the 3-D space of our everyday experience and into higher dimensions.
Equiangular lines are much more than a curiosity — they’re an almost elemental way to think about geometry. Maximal constructions of equiangular lines often align perfectly with the vertices of highly symmetric shapes, which make them a way to discover the existence of those shapes in the first place. In addition, radiating equiangular lines would pass through the surface of a surrounding sphere at equidistant points. This property makes the lines important for so-called spherical codes, which have important applications in applied mathematics and computer science.
Last spring a team of mathematicians found the maximum number of equiangular lines possible in any dimension, given certain conditions. They proved that that number is much smaller than previous best estimates. Benny Sudakov, a professor of mathematics at the Swiss Federal Institute of Technology Zurich and one of the lead authors, credits the breakthrough to the wide range of mathematical techniques he and his coauthors were able to apply to the problem.
“It’s like when you’re cooking something, we suddenly found we had the right ingredients,” said Sudakov.
Quanta Magazine: A New Path to Equal-Angle Lines, Kevin Hartnett
Comments