 |
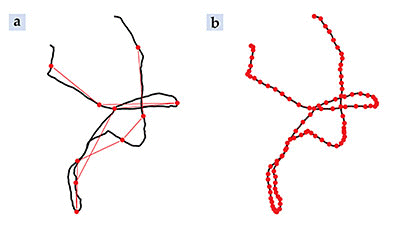
Figure 1. Brownian motion trajectories. When examined at modest measurement rates (a), the observed positions (red dots) of particles executing Brownian motion appear to lie on the jerky trajectory illustrated in red. The black curve shows the underlying particle path. (b) Measurements at finer time scales reveal that the particle path is in fact built from short bursts of constant velocity motion.
Citation: Phys. Today 68, 1, 56 (2015); http://dx.doi.org/10.1063/PT.3.2665
It's always exciting when I recognize and actually know the authors!
Dr. Mark G. Raizen is the Sid W. Richardson Foundation Regents Chair of Physics and Professor of Physics at the University of Texas, Austin.
Dr. Tongcang Li received his PhD under Mark's guidance and is now Assistant Professor of Physics and Astronomy/Assistant Professor of Electrical and Computer Engineering at Purdue University. They were both kind enough when Dr. Li was completing his graduate degree to give Cassandra and I a tour of their lab and impressive work at UT.
Mark has pioneered, in his own words, a "general methods to control the motion of atoms and molecules. This work will be used to test very basic questions in physics, and will also find real-life applications," which is a modest understatement! First to do this was former Department of Energy Secretary and Nobel Laureate Dr. Steven Chu. The process in the Raizen Group is a vast improvement on this impressive achievement. An excerpt of the article is below; explore the article at the link for "optical tweezers": think James Clerk Maxwell's "demon" thought experiment. Keep in mind real-life applications going forward. Nicely done, gentlemen: I applaud your great research and a well-written presentation. I thank you for your permission to post this.
Particles undergoing Brownian motion move with constant velocity between Brownian kicks. Albert Einstein predicted the velocity distribution, but he wrongly thought his result would never be experimentally confirmed.
Brownian motion, the seemingly random wiggle-waggle of particles suspended in a liquid or gas, was first systematically studied by Robert Brown in 1827 and described in the Philosophical Magazine the next year (volume 4, page 161). When Brown used a microscope to look at particles from pollen grains immersed in water, he “observed many of them very evidently in motion.” It looked like the particles were alive, so vigorously did they move.
The phenomenon of Brownian motion was first explained by Albert Einstein in 1905 as a consequence of the thermal motion of surrounding fluid molecules. Einstein’s theory predicts that Brownian particles diffuse; as a consequence, their mean-square displacement 〈(Δ x)2〉 = 2 Dt in each dimension is proportional to a diffusion coefficient D and the measured time interval t. As illustrated in figure 1 a, the motion of Brownian particles looks like a jerky and unpredictable dance, and the sudden changes in direction and speed seem to indicate that velocity is not defined. Moreover, the mean velocity
〈 v〉 ≡ 〈(Δ x)2〉 1/2/ t = (2 D/ t) 1/2 diverges as t approaches 0. If you think all that is strange, you are in good company: Einstein felt the same way.
Physics Today: The measurement Einstein deemed impossible
Mark G. Raizen and Tongcang Li
Related #P4TC Links:
Improved Isotope Enrichment, July 1, 2014
Einstein, Entropy and Information, March 23, 2013
Brownian Motion...Einstein "wrong..ish", May 16, 2011
Maxwell's Demon & information-to-energy, November 16, 2010
Comprehensive Control of Atomic and Molecular Motion, August 23, 2010
Comments